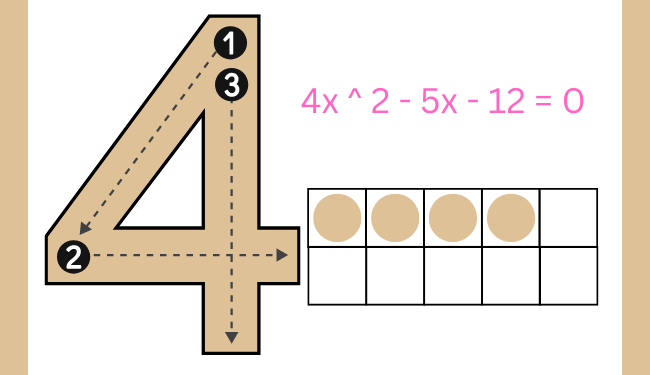
The quadratic equation, a cornerstone in algebra, often appears intimidating to students and enthusiasts alike. The equation 4x^2 – 5x – 12 = 0 is a quintessential example that encompasses the fundamental principles of solving quadratic equations. This article delves deep into understanding and solving this equation, offering expert techniques to demystify the process and build confidence in tackling similar problems.

Understanding the Quadratic Equation
Quadratic equations take the general form ax^2 + bx + c = 0, where ‘a,’ ‘b,’ and ‘c’ are constants. In the equation 4x^2 – 5x – 12 = 0, we identify ‘a’ as 4, ‘b’ as -5, and ‘c’ as -12. The goal is to find the values of ‘x’ that satisfy the equation, known as the roots of the equation.

Quadratic equations can have two real roots, one real root, or two complex roots, depending on the discriminant (b^2 – 4ac). The nature of the origins provides insights into the equation’s solutions, guiding us in choosing the appropriate method to solve it.
The Discriminant and Its Significance
Before diving into solving 4x ^ 2 – 5x – 12 = 0, it’s crucial to understand the discriminant, which is calculated as D = b^2 – 4ac. The discriminant determines the nature of the roots:
- If D > 0, the equation has two distinct real roots.
- If D = 0, the equation has one real root (a repeated root).
- If D < 0, the equation has two complex roots.
For our equation, the discriminant is calculated as follows: 𝐷=(−5)2−4(4)(−12)=25+192=217D=(−5)2−4(4)(−12)=25+192=217
Since the discriminant is positive (217 > 0), the equation 4x^2 – 5x – 12 = 0 has two distinct real roots. This knowledge reassures us that our solutions will be real numbers, paving the way for solving the equation using various techniques.
Factoring the Quadratic Equation
Factoring is a method that involves expressing the quadratic equation as a product of two binomials. This method works efficiently when the equation is easily factorable. However, not all quadratic equations can be factored readily, and additional techniques might be required.
For 4x^2 – 5x – 12 = 0, we seek two numbers that multiply to (ac) = 4(-12) = -48 and add to ‘b’ = -5. These numbers are 3 and -16. Rewriting the middle term using these numbers, we get: 4𝑥2+3𝑥−16𝑥−12=04x2+3x−16x−12=0
Next, we group the terms and factors by grouping: (4𝑥2+3𝑥)+(−16𝑥−12)=0(4x2+3x)+(−16x−12)=0 𝑥(4𝑥+3)−4(4𝑥+3)=0x(4x+3)−4(4x+3)=0
Factoring out the common binomial (4x + 3), we obtain: (4𝑥+3)(𝑥−4)=0(4x+3)(x−4)=0
Setting each factor to zero gives the solutions: 4𝑥+3=0⇒𝑥=−344x+3=0⇒x=−43 𝑥−4=0⇒𝑥=4x−4=0⇒x=4
Thus, the roots of the equation are 𝑥=−34x=−43 and 𝑥=4x=4.

The Quadratic Formula
When factoring is not straightforward, the quadratic formula offers a reliable method to solve any quadratic equation. The quadratic formula is given by: 𝑥=−𝑏±𝑏2−4𝑎𝑐2𝑎x=2a−b±b2−4ac
Applying this formula to 4x^2 – 5x – 12 = 0, we substitute ‘a’ = 4, ‘b’ = -5, and ‘c’ = -12: 𝑥=−(−5)±(−5)2−4(4)(−12)2(4)x=2(4)−(−5)±(−5)2−4(4)(−12) 𝑥=5±25+1928x=85±25+192 𝑥=5±2178x=85±217
This results in two distinct roots: 𝑥=5+2178x=85+217 𝑥=5−2178x=85−217
These roots are the solutions to the equation, and their exact values can be approximated using a calculator for practical applications.
Completing the Square
Completing the square is another method for solving quadratic equations. This method is handy for understanding how the equation transforms into vertex form. The process involves creating a perfect square trinomial from the quadratic equation.
Starting with 4x^2 – 5x – 12 = 0, we first divide by ‘a’ (4) to normalize the coefficient of x^2: 𝑥2−54𝑥−3=0x2−45x−3=0
Next, we isolate the constant term: 𝑥2−54𝑥=3x2−45x=3
To complete the square, we add and subtract (𝑏2𝑎)2(2ab)2: 𝑥2−54𝑥+(58)2=3+(58)2x2−45x+(85)2=3+(85)2 𝑥2−54𝑥+2564=3+2564x2−45x+6425=3+6425 (𝑥−58)2=21764(x−85)2=64217
Taking the square root of both sides, we obtain: 𝑥−58=±21764x−85=±64217 𝑥=58±2178x=85±8217
This simplifies to 𝑥=5+2178x=85+217 𝑥=5−2178x=85−217
These solutions match those obtained using the quadratic formula, demonstrating the consistency and reliability of different methods in solving quadratic equations.
Graphical Interpretation
Visualizing the quadratic equation on a graph provides a deeper understanding of the solutions. The graph of a quadratic equation is a parabola, which can open upwards or downwards depending on the sign of ‘a.’ For 4x^2 – 5x – 12 = 0, ‘a’ is positive (4), so the parabola opens upwards.
The roots of the equation, 𝑥=−34x=−43 and 𝑥=4x=4, correspond to the x-intercepts of the parabola. The vertex of the parabola, given by the formula 𝑥=−𝑏2𝑎x=−2ab, provides the axis of symmetry. For our equation: 𝑥=−−52(4)=58x=−2(4)−5=85
Substituting 𝑥=58x=85 into the equation to find the y-coordinate of the vertex: 𝑦=4(58)2−5(58)−12y=4(85)2−5(85)−12 𝑦=4(2564)−258−12y=4(6425)−825−12 𝑦=10064−20064−76864y=64100−64200−64768 𝑦=100−200−76864y=64100−200−768 𝑦=−86864=−13.5625y=64−868=−13.5625
The vertex of the parabola is (58,−13.5625)(85,−13.5625), indicating the lowest point of the graph. Understanding the graphical interpretation helps visualize the quadratic equation’s behavior and confirm the solutions’ accuracy.

Conclusion
Solving the quadratic equation 4x^2 – 5x – 12 = 0 involves understanding various techniques, each offering a unique approach to finding the roots. From factoring and the quadratic formula to completing the square and graphical interpretation, mastering these methods equips us with the tools to tackle any quadratic equation confidently.
Whether you’re a student grappling with algebra or an enthusiast seeking to deepen your mathematical prowess, these expert techniques provide a comprehensive guide to demystifying quadratic equations. Embrace these strategies, and you’ll find that solving equations like 4x^2 – 5x – 12 = 0 becomes a manageable and rewarding challenge.