The Gram-Schmidt Calculator is a vital tool in mathematics and computer science, specifically designed to perform the Gram-Schmidt Orthogonalization Process. This process is crucial for converting a set of vectors into an orthogonal or orthonormal set, which is fundamental in various applications, including statistics, physics, and numerical analysis. In this comprehensive guide, we will explore the significance of the Gram Schmidt Calculator, its applications, how it operates, and its advantages over traditional methods.
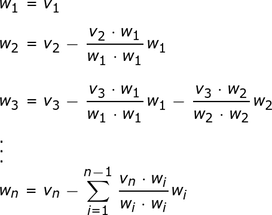
Understanding the Gram-Schmidt Process
The Basics of Vector Orthogonalization
The Gram-Schmidt process is a method used to orthogonalize vectors in an inner product space, such as ℝⁿ. This process takes a linearly independent set of vectors and converts them into a set of orthogonal (perpendicular to each other) and of unit length (if orthonormalization is desired). The orthogonalization is fundamental because orthogonal vectors simplify many mathematical and computational problems, particularly those involving vector spaces and matrix algebra.
Mathematical Foundation
The process begins with vectors {v1, v2, …, vn}. The first step is to set the first orthogonal vector u1 equal to v1. Subsequent vectors are then computed by subtracting from each subsequent vector the projection of that vector onto each of the previously computed orthogonal vectors. Mathematically, this is expressed as: ��=��−∑�=1�−1proj����uk=vk−∑j=1k−1projujvk where proj����projujvk is the projection of ��vk onto ��uj. This method ensures that each ��uk is orthogonal to all previous ��ones.
Practical Application Scenarios
Orthogonal vectors are used in various practical scenarios, such as solving systems of linear equations, computer graphics, signal processing, and machine learning. For instance, in QR decomposition, which is used to solve linear least squares problems, the Gram-Schmidt process is employed to factorize a matrix into an orthogonal and upper triangular matrix.

The Role of a Gram Schmidt Calculator
Simplifying Complex Calculations
The manual calculation of the Gram-Schmidt process is feasible but cumbersome, especially with larger sets of vectors and higher dimensions. A Gram Schmidt Calculator automates these calculations, reducing the potential for human error and significantly speeding up the process. This makes the calculator an indispensable tool for students, educators, and professionals working with complex vector and matrix calculations.
How the Calculator Works
Typically, a Gram-Schmidt Calculator requires the user to input the vectors in a given format (such as comma-separated values or matrix form). The calculator then processes these inputs using the Gram-Schmidt algorithm to produce orthogonal (or orthonormal) vectors. Advanced calculators might also provide step-by-step explanations of the calculations, enhancing understanding and learning.
Accessibility and Efficiency
Many online platforms offer free access to Gram-Schmidt calculators, making this powerful mathematical tool available to a wider audience. These calculators are used for educational purposes and integrated into professional software tools used in engineering and data analysis.

Advantages of Using a Gram-Schmidt Calculator
Accuracy and Reliability
The main advantage of using a Gram Schmidt Calculator is the accuracy it brings to the calculations. Mathematical computations, especially those involving floating-point arithmetic, are prone to errors when done manually. The calculator minimizes these errors, providing reliable results quickly.
Time-Saving
Manually performing orthogonalization can be time-consuming for students and professionals who deal with large datasets or complex vector spaces. A calculator streamlines this process, freeing time to focus on other aspects of their projects or studies.
Educational Value
For educational purposes, the Gram-Schmidt Calculator is an excellent tool for demonstrating the orthogonalization process. It allows students to experiment with different sets of vectors and see the immediate impact of changes, which can enhance their understanding and retention of the concept.

Conclusion
The Gram-Schmidt Calculator is more than just a computational tool; it is a pivotal element in simplifying and applying mathematical concepts in real-world scenarios. Whether for educational or professional use, this calculator facilitates a deeper understanding and efficient handling of vector orthogonalization, making “Efficient Gram Schmidt Calculator: Orthogonalization Made Easy” a title and a reality in the mathematical community. By leveraging such tools, we can ensure that complex mathematical processes become accessible, accurate, and efficient, supporting continued advancement in science, technology, engineering, and mathematics.